Условия всех задач из категории B7

Первый счет возник тогда, когда человеку потребовалось информировать своих сородичей о количестве обнаруженных им предметов. Сначала первобытные люди просто различали, один предмет перед ними распложен или нет. Если предметов было больше одного, то говорили «много». Первыми понятиями арифметики были термины «меньше», «больше» и «столько же». Если одно сообщество первобытных людей хотело обменять пойманных ими рыб на стрелы, принадлежащие другому сообществу, то достаточно было положить рядом с каждой рыбой по стреле, чтобы обмен (получается бартер) между племенами состоялся.

В конце концов, человек обратил внимание на собственную руку, на которой располагалось ровно пять пальцев. С их помощью можно было считать до пяти, а если задействовать обе руки, то и до десяти. Одна из таких систем счета впоследствии и стала общеупотребительной – десятичная.

Система счисления – специфический формат записи чисел с использованием некого набора специальных знаков.

Основание системы счисления – количество цифр (знаков), используемых в записи числа.

Классификация систем счисления:

• позиционные;

• непозиционные;

• смешанные.

Специфика позиционных систем счисления: один и тот же числовой знак в записи любого числа может принимать различные значения, в зависимости от занимаемой им позиции.

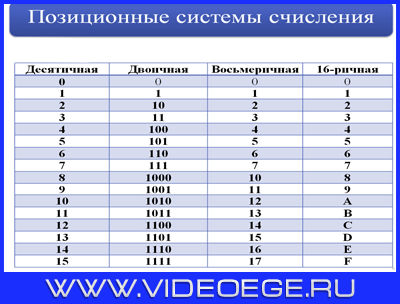
Наиболее популярные позиционные системы счисления:

• двоичная;

• восьмеричная;

• десятичная;

• шестнадцатеричная.

Наиболее популярные операции, которые требуется проводить при решении задач из данной категории:

• преобразование числа из одной позиционной системы счисления в другую позиционную систему счисления;

• составление и решение простейших математических уравнений, для выявления основания системы счисления;

• перебор определенного набора оснований систем счисления, для детерминации только тех чисел, удовлетворяющих поставленным критериям.

Для успешного решения задач из данной категории вы должны:

1. составить позиционное уравнение (некая информатическая модель математического уравнения), основанное на том, что рассматривается одно и то же число;

2. проверить полученные корни (данные корни представляют собой значения для искомых оснований систем счислений), и, если потребуется, исключить неподходящие основания системы счисления.

Дано:
в системе счисления с некоторым основанием десятичное число 81 записывается в виде 100.

Найти:
укажите это основание

Дано:
в системе счисления с некоторым основанием десятичное число 51 записывается в виде 102

Найти:
укажите это основание

Дано:
в системе счисления с некоторым основанием десятичное число 52 записывается в виде 202.

Вопрос:
укажите это основание

Дано:
в системе счисления с некоторым основанием десятичное число 103 записывается в виде 205.

Вопрос:
укажите это основание