Условия всех задач из категории B3

В технике используется множество способов, с помощью которых получают различные графические изображения. Наиболее употребимые из них создавались и совершенствовались в течение многих веков.

К сожалению, история сохранила не много исторических документов, по которым возможно проследить эволюцию графических способов отображения информации. Однако совершенно очевидно, что их основы закладывались в глубокой древности.

Рассматривая историю развития изображений, принятых в технике, следует обратиться к истокам — первобытным рисункам и древним пиктограммам. Именно в них берет свое начало, зарождается и формируется графический язык, основой которого являются способы изображений.

График – множество точек координатной плоскости. Любой график отражает какой-либо процесс или какую-либо зависимость.

Диаграмма – графическое представление данных, позволяющее в удобной форме проанализировать соотношение некоторых зависимых величин.

Фундаментальные типы диаграмм:

• линейная;

• областная;

• гистограмма;

• круговая;

• радиальная;

• картодиаграмма.

Как правило, в задачах из данной категории, в исходных данных присутствует электронная таблица MS Excel, содержащая некоторую совокупность данных. На основе предложенных данных строится диаграмма, и требуется детерминировать какое-либо значение. Решение сводится к тому, чтобы понять смысл входных данных и найти соответствие между входными данными и фрагментами построенной диаграммы.

Нередко приходится прибегать к основным математическим функциям программы MS Excel для нахождения искомой величины.

Для успешного решения задач из данной категории вы должны:

1. проанализировать представленные диаграммы. Как правило, часть из них выражают количественную оценку сущностей, а часть относительную оценку сущностей;

2. как правило, следует узнать общее количество рассматриваемых сущностей (школьники, мячики, тетради и т. п.);

3. последовательно перебирать предложенные утверждения и "накладывать" их на заданные диаграммы. Только единственное утверждение является корректным. Как только подходящее утверждение будет найдено, закончить перебор и выписать ответ.

Дано:
все ученики старших классов (с 9-го по 11-й) участвовали в школьной спартакиаде. По результатам соревнований каждый из них получил от 0 до 3-х баллов.
На диаграмме I отражено распределение учеников по классам, а на диаграмме II — количество учеников, набравших баллы от 0 до 3-х. На  обеих диаграммах каждый ученик учтён только один раз.

Имеются четыре утверждения: 

1. среди учеников 9-го класса есть хотя бы один, кто набрал 0 баллов;

2. все 11-классники набрали больше 0 баллов;

3. все ученики 11-го класса могли набрать ровно один балл;

4. среди учеников 10-го класса есть хотя бы один, кто набрал 2 балла.

Вопрос:
какое из этих утверждений следует из анализа обеих диаграмм? 

Дано:
все ученики старших классов (с 9-го по 11-й) участвовали в школьной спартакиаде. По результатам соревнований каждый из них получил от 0 до 3-х баллов.
На диаграмме I отражено распределение учеников по классам, а на диаграмме II — количество учеников, набравших баллы от 0 до 3-х. На  обеих диаграммах каждый ученик учтён только один раз.

Имеются четыре утверждения: 

1. среди учеников 9-го класса есть хотя бы один, набравший 2 или 3 балла;

2. все ученики, набравшие 0 баллов, могут быть 9-классниками;

3. все 10-классники могли набрать ровно по 2 балла;

4. среди набравших 3 балла нет ни одного 10-классника.

Вопрос:
какое из этих утверждений следует из анализа обеих диаграмм?

Дано:
в магазине продаются мячи четырех цветов (синие, зеленые, красные и желтые) и трех размеров (большие, средние и маленькие).
На диаграмме I отражено количество мячей разного размера, а на диаграмме II - распределение мячей по цветам.

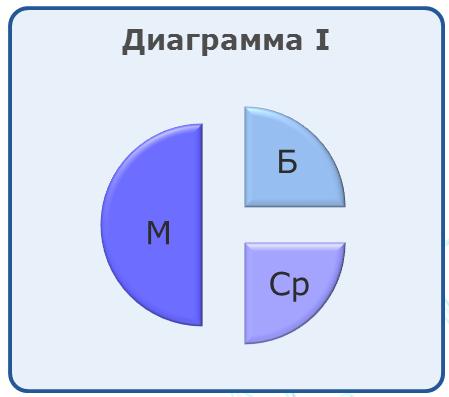
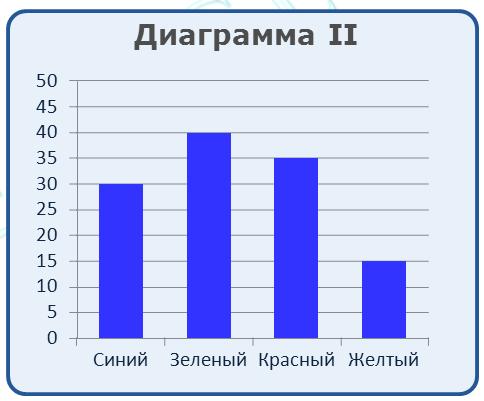
Имеются четыре утверждения: 

1. среди больших мячей должен быть хотя бы один синий;

2. ни один мяч среднего размера не может быть красным;

3. все маленькие мячи могут быть зелеными;

4. все зеленые мячи могут быть маленькими.

Вопрос:
какое из этих утверждений следует из анализа обеих диаграмм?

Дано:
в магазине продаются мячи четырех цветов (синие, зеленые, красные и желтые) и трех размеров (большие, средние и маленькие).
На диаграмме I отражено количество мячей разного размера, а на диаграмме II - распределение мячей по цветам.

Имеются четыре утверждения: 

1. все маленькие мячи могут быть синими или желтыми;

2. среди больших мячей найдется хотя бы один красный;

3. среди маленьких мячей найдется хотя быть один зеленый или красный;

4. все красные мячи могут быть среднего размера.

Вопрос:
какое из этих утверждений следует из анализа обеих диаграмм?